Крововилив в око: симптоми, причини та лікування стану
Червона пляма в оці, що з’явилась після важкого чхання, може налякати кожного. Багато з нас хоч раз у житті помічали дивне почервоніння білка ока, яке виникло без видимої причини. Це може бути крововилив – стан, який потребує уваги та правильних дій.
Що таке крововилив в око?
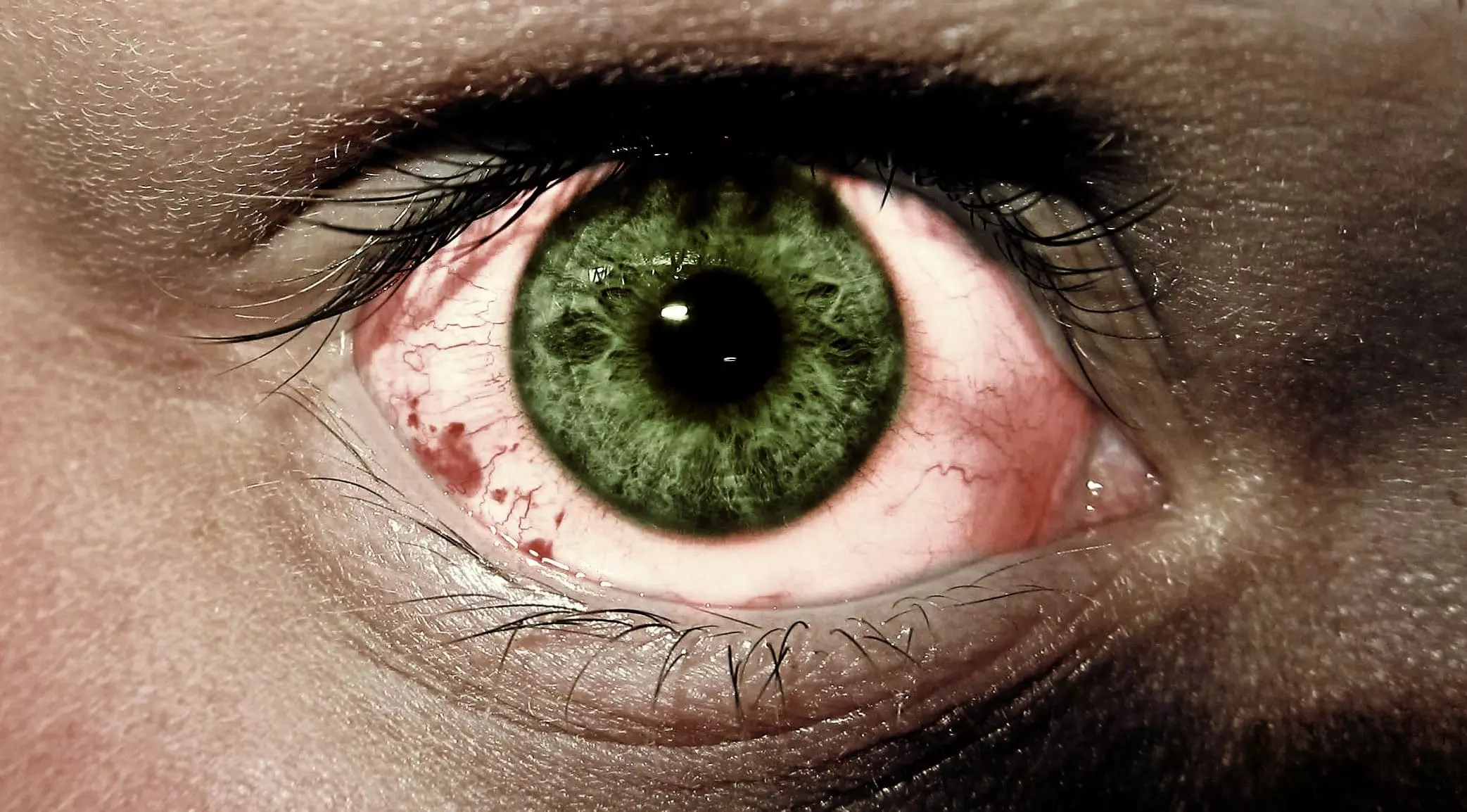
Коли маленька судина в оці лопається, кров виливається під кон’юнктиву або в інші структури ока. Залежно від місця, розрізняють різні типи. Субкон’юнктивальний крововилив – найпоширеніший тип, коли кров збирається під прозорою оболонкою ока. Виглядає як яскраво-червона пляма на білку. При крововиливі у сітківку кров потрапляє в тканини сітківки, що може серйозно загрожувати зору. Гемофтальм означає накопичення крові в склоподібному тілі, яке заповнює око зсередини.
Причини крововиливу в око
Раптовий крововилив може статися з різних причин. Травми ока часто викликають крововилив – це може бути удар м’ячем під час гри або гілкою під час прогулянки в парку. Підвищений тиск також становить ризик, адже гіпертонічний криз часто провокує розрив судин. Цукровий діабет ушкоджує дрібні судини не тільки в нирках, але й в очах, роблячи їх більш вразливими. Порушення згортання крові через прийом деяких ліків або через певні хвороби також підвищують ризик крововиливу. Навіть сильний кашель, чхання чи підняття важкого може спричинити крововилив через різке підвищення тиску в судинах.
Симптоми та ознаки
Побачити червону пляму на білку ока можна в дзеркалі, але інші прояви крововиливу також важливі. Пацієнти часто скаржаться на відчуття стороннього тіла або піску в оці. Може виникати легкий біль або дискомфорт, який посилюється при русі очного яблука. Погіршення зору особливо характерне при крововиливах у сітківку, коли людина бачить розмито або з викривленнями. Багато пацієнтів описують темні плями або “мушки” перед очима. При субкон’юнктивальному крововиливі зір зазвичай не страждає, а от гемофтальм може серйозно його погіршити.
 Діагностика
Діагностика
Для правильної оцінки стану лікар проведе:
- Зовнішній огляд ока з використанням щілинної лампи
- Офтальмоскопію – огляд сітківки та інших внутрішніх структур
- Оптичну когерентну томографію (ОСТ) для детального вивчення сітківки
- Флюоресцентну ангіографію у складних випадках
Не відкладайте візит до офтальмолога, особливо якщо крововилив виник без причини або супроводжується іншими симптомами.
Лікування
Більшість субкон’юнктивальних крововиливів зникають самі за 1-2 тижні. Лікування може включати:
- Очні краплі для зменшення дискомфорту
- Холодні компреси для зменшення набряку
- Відмову від контактних лінз на час лікування
При серйозних крововиливах у сітківку або склоподібне тіло може знадобитися:
- Лазерна коагуляція для зупинки кровотечі
- Вітректомія – хірургічне видалення крові зі склоподібного тіла
Можливі ускладнення
Без належного лікування крововилив може призвести до:
- Стійкого погіршення зору
- Відшарування сітківки
- Підвищення внутрішньоочного тиску
- Рубцювання тканин
 Профілактика
Профілактика
Щоб зменшити ризик крововиливів, важливо дотримуватися кількох простих правил. Контролюйте артеріальний тиск регулярними вимірюваннями та дотриманням призначеного лікування. Носіть захисні окуляри при роботі з ризиком травм, наприклад, під час ремонту чи роботи в майстерні. Проходьте регулярні огляди у офтальмолога, особливо якщо у вас діабет або інші хронічні захворювання. Обов’язково повідомляйте лікаря про прийом препаратів, що впливають на згортання крові, таких як аспірин або варфарин.
Коли звертатися до лікаря
Негайно зверніться до офтальмолога, якщо крововилив виник після травми ока, адже це може бути ознакою серйозніших пошкоджень. Також потребує медичної уваги ситуація, коли ви відчуваєте біль в оці, який не минає протягом кількох годин. Тривожним сигналом є погіршення зору, особливо раптове затуманення або випадіння частини поля зору. Якщо крововиливи повторюються часто, це теж причина для візиту до спеціаліста, оскільки може вказувати на приховане захворювання.
Крововилив в око часто виглядає страшніше, ніж є насправді. Більшість дрібних крововиливів проходять без наслідків, але важливо перевірити, чи немає серйозніших проблем. Не соромтеся звернутися до офтальмолога – своєчасна консультація допоможе зберегти найцінніше – ваш зір.
Пам’ятайте, що здоров’я очей – це частина загального здоров’я. Регулярні перевірки допоможуть уникнути багатьох проблем або виявити їх на ранній стадії, коли лікування найефективніше.

 Діагностика
Діагностика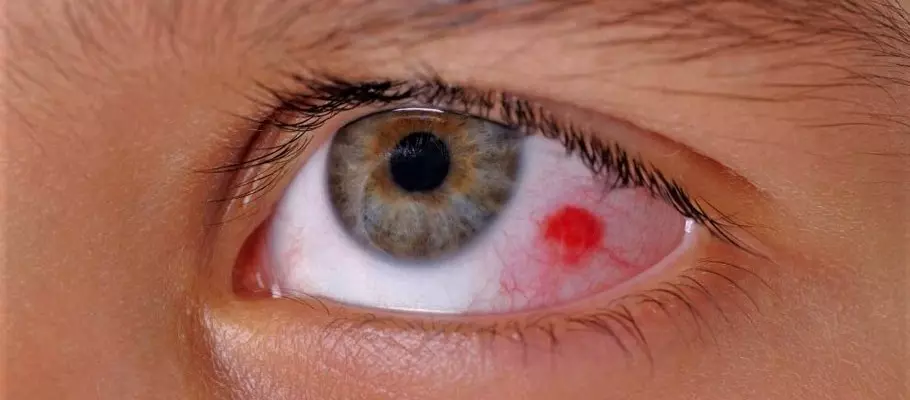 Профілактика
Профілактика